• (AND-OR === NAND-NAND, OR-AND === NOR-NOR)이므로 (AND-OR/OR-AND보다는 NAND-NAND/NOR-NOR를 쓰는게 더 저렴하다)

  • 여러가지 Boolean Algebra의 정리를 이용해서 Logic minimization(# of gates, # of gate inputs)하는데 어떤 정리를 먼저 쓰냐에 따라 결과가 다르기 때문에 쉽지가 않다.

  • Don’t care condition: F값이 0/1이 정의되지 않는 경우로 0/1로 나눠서 2번 풀어서 비용을 비교해야함

Useful Theorems

    1. x + xy = x, x + x’y = x+y
1
2


    1. ab + b’c + ac = ab + b’c
1
2


    1. if ab’ + a’b = ac’ + a’c, then b=c
1
2
3
4
5
6
ab' + a'b = ac' + a'c이 같다면 두 항을 xor취했을 때 결과가 0이 나와야 한다
-> ab' + a'b = ac' + a'c
-> (a xor b) xor (a xor c) = 0
-> a xor a xor b xor c = 0
-> b xor c = 0
-> hence, b = c
    1. if a = b, then a xor c = b xor c
1
2
3
4
5
3번과 마찬가지로, xor 이용
-> (a xor c) xor (b xor c)
-> a xor b xor c xor c
-> a xor b = 0
-> hence, a xor c = b xor c
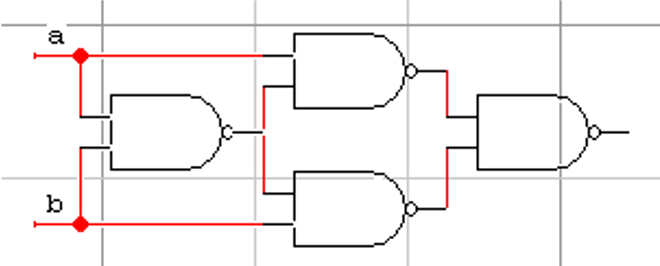
    1. find the expression of f
1
2


    1. find the product-of-sum form of f = wxy + wx’y’ + w’xy’

카르노맵

  • 이런 문제를 쉽게 풀고자 나온게 카르노맵
  • 카르노맵의 출발은 AB’ + AB = A으로 Canonical Form을 나타내기에 충분하다라는 것
  • 보통 입력수가 4개 이하일 때 카르노맵을 이용해서 문제를 푼다.
  • 이웃한 1을 그룹지어 항을 만든다
  • 테이블을 만들때, 변수가 하나씩 바뀌어야 한다
1
2
(00, 01, 11, 10) // O
(00, 01, 10, 11) // X
  • 각 끝 행과 열은 처음 행과 열로 그룹지을 수 있다